
Deducción de la fórmula
Para calcular una integral de la forma
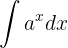
debemos recordar que la derivada de una función exponencial está dada por

Por lo tanto, la integral de 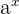 se calcula mediante:
se calcula mediante:

Así, concluimos que la fórmula de la integral para 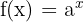 es
es

Para el caso particular, donde  (número de Euler), tenemos
(número de Euler), tenemos
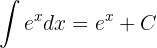
Por último, si  es una función, entonces la fórmula con sustitución es
es una función, entonces la fórmula con sustitución es

Y cuando la base es  , tenemos
, tenemos

Observemos que 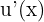 debe estar multiplicando al diferencial.
debe estar multiplicando al diferencial.
Ejemplos
1 Calcula la siguiente integral
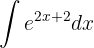
Observemos que la base del exponencial es  . Asimismo, tenemos que
. Asimismo, tenemos que 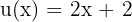 . Como
. Como 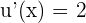 , entonces necesitamos multiplicar al diferencial por 2:
, entonces necesitamos multiplicar al diferencial por 2:
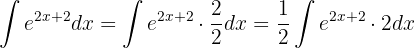
Con esto, ya podemos calcular la integral:
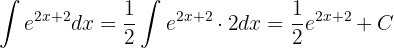
2 Determina la siguiente integral
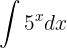
Ahora, observemos que la base es 5. Además, el argumento de la exponencial es simplemente  . Por lo tanto, podemos utilizar la fórmula directamente con
. Por lo tanto, podemos utilizar la fórmula directamente con  :
:
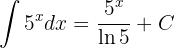
3 Calcula la siguiente integral de producto de exponenciales:
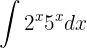
Recordemos que  ya que tienen el mismo exponente. Por lo tanto, la integral se calcula como
ya que tienen el mismo exponente. Por lo tanto, la integral se calcula como
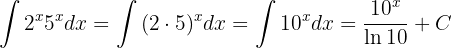
Es importante notar que, aunque se podría llegar al mismo resultado utilizando la integral por partes, el procedimiento sería más tedioso.
4 Obtén la siguiente integral
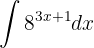
Notemos que 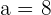 y que
y que  . Así, tenemos que
. Así, tenemos que  , por lo que tenemos que multiplicar el diferencial por 3 (al mismo tiempo hay que dividir por 3 para que la función siga siendo la misma):
, por lo que tenemos que multiplicar el diferencial por 3 (al mismo tiempo hay que dividir por 3 para que la función siga siendo la misma):
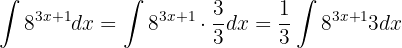
Por tanto, la integral es

5 Determina la siguiente integral
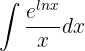
Hay dos maneras de terminar esta integral. La más sencilla es notar que 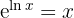 , por lo tanto,
, por lo tanto,
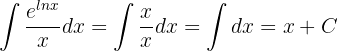
Notemos que el dominio de 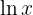 es
es 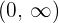 . Por lo tanto, la solución también está restringida a este dominio.
. Por lo tanto, la solución también está restringida a este dominio.
Sin embargo, como estamos utilizando la fórmula de la integral exponencial, entonces también podemos utilizarla y debemos llegar al mismo resultado. En este caso, notemos que  . Así,
. Así,  (el cuál ya está multiplicando al diferencial), es decir,
(el cuál ya está multiplicando al diferencial), es decir,
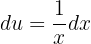
Por tanto,
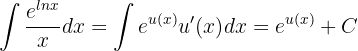
pero, como  , entonces tenemos
, entonces tenemos
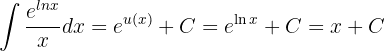
ya que 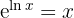 .
.
6 Calcula la siguiente integral

Observemos que  . Por lo tanto,
. Por lo tanto,

el cuál ya está multiplicando al diferencial. De este modo,

7 Determina la siguiente integral

Observemos que 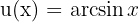 . Por tanto, esta integral es bastante sencilla si logramos recordar que
. Por tanto, esta integral es bastante sencilla si logramos recordar que
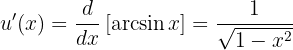
De este modo, la integral se vuelve














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio 26 el resultado no se ve bien, como quedaria?
Disculpa pero no hay ejercicio 26, solo llega al 20.
estan la mitad de los ejercicios incorrectos, revisarlos por favor
Podrías indicarnos que ejercicios están mal, pues ya revise y no encontre los errores.
En el ejercicio 13 que es la integral de x^2 * ln(x^2), al hacerlo por partes hace bien lo de coger como u=ln(x^2), pero al coger x^2 como v’ se equivoca y lo coge como x^3
Una disculpa ya se corrigió.
En la pagina no deja ver las respuestas, me parece que es un error de vosotros a ver si lo podeis arreglar, mil gracias
Hola, Pancracio:
Las soluciones ya aparecen correctamente 🙂
Un saludo
Estudio carrera de ingeniería pero me cuesta mucho las matemáticas ¿ algún consejo? O tips