Calcular las integrales trigonométricas:
1 
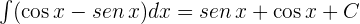
2
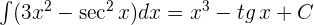
3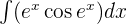
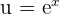 , tenemos una integral inmediata, entonces:
, tenemos una integral inmediata, entonces:
4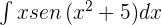
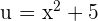 , tenemos:
, tenemos: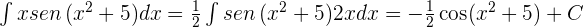
5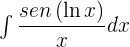
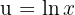 , tenemos:
, tenemos:
6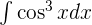
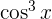 y utilizamos la identidad trigonométrica
y utilizamos la identidad trigonométrica 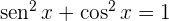 , entonces:
, entonces: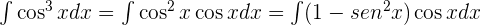
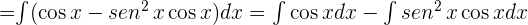
Hacemos un cambio de variable
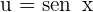 y
y  a la segunda integral
a la segunda integral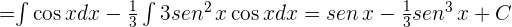
7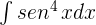
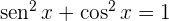 y obtenemos:
y obtenemos:

utilizando la identidad
 para la tercer integral, tenemos:
para la tercer integral, tenemos:


8
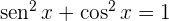 , entonces:
, entonces: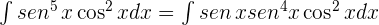
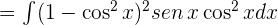
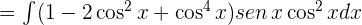
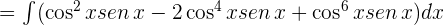
Hacemos los cambios de variables para cada una de las integrales y obtenemos:

9
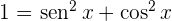 , tenemos:
, tenemos:
Haciendo los cambios de variable a cada integral tenemos:

10


11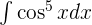
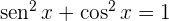
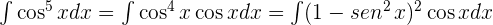

Haciendo los cambios de variables a cada integral, tenemos:

12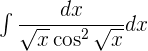
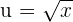
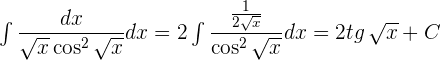
13
 , tenemos:
, tenemos:
Usando el cambio de variable
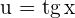 y
y 

14
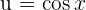 para la primer integral, tenemos:
para la primer integral, tenemos:

15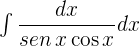
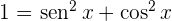 y separando las integrales, tenemos:
y separando las integrales, tenemos:
Haciendo los cambios de variables para cada integral, tenemos:




Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio 26 el resultado no se ve bien, como quedaria?
Disculpa pero no hay ejercicio 26, solo llega al 20.
estan la mitad de los ejercicios incorrectos, revisarlos por favor
Podrías indicarnos que ejercicios están mal, pues ya revise y no encontre los errores.
En el ejercicio 13 que es la integral de x^2 * ln(x^2), al hacerlo por partes hace bien lo de coger como u=ln(x^2), pero al coger x^2 como v’ se equivoca y lo coge como x^3
Una disculpa ya se corrigió.
En la pagina no deja ver las respuestas, me parece que es un error de vosotros a ver si lo podeis arreglar, mil gracias
Hola, Pancracio:
Las soluciones ya aparecen correctamente 🙂
Un saludo
Estudio carrera de ingeniería pero me cuesta mucho las matemáticas ¿ algún consejo? O tips