La integral definida es un caso de la integral utilizado para determinar el valor de las áreas delimitadas por una gráfica dentro de un intervalo y el eje horizontal. Sele puede encontrar en diversas áreas y contextos como la biología (en crecimiento de poblaciones), robótica (algoritomo de seguimiento de lineas), arquitectura (volúmenes de sólidos), etc, más adelante se dará un ejemplo específico de una aplicación.
Formalmente se define de la siguiente manera:

Definición de la integral definida
Dada una función f(x) de una variable real x y un intervalo [a,b] de la recta real, la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las líneas verticales x = a y x = b.

Se representa por  .
.
 es el signo de integración.
es el signo de integración.- a es el límite inferior de la integración.
- b es el límite superior de la integración.
 es el integrando o función a integrar.
es el integrando o función a integrar. es el diferencial de x y nos indica cuál es la variable de la función que se integra.
es el diferencial de x y nos indica cuál es la variable de la función que se integra.
Propiedades de la integral definida
1 El valor de la integral definida cambia de signo si se permutan los límites de integración.

Esta propiedad nos puede servir para no operar con signos negativos.
Ejemplo:

2 Si los límites de integración coinciden, la integral definida vale cero.

En realidad, al tener el mismo límite de integración en ambos extremos no existe ningún área a calcular, es por eso que la integral es igual a cero en este caso.
Ejemplo:


Al estar el punto c entre a y b sobre el eje de las abcisas, el área limitada por el intervalo [a,b] es la suma de las áreas limitadas por [a,c] y [c,d], lo mismo ocurre con el valor de la integral.
Ejemplo:
Para 7 que pertenece al intervalo [3,10]

4 La integral definida de una suma de funciones es igual a la suma de integrales.

Esta propiedad nos puede servir para no tener expresiones muy largas dentro de una misma integral y así manipular y hacer cálculos más facilmente , o en el otro caso, agrupar expresiones para un cálculo más cómodo.
Ejemplo:
Para  y
y  ,
,

5 La integral del producto de una constante k por una función es igual a la constante k multiplicada por la integral de la función.

Esto es sacar la constante fuera de la integral.
Ejemplo:
Para la constante k=3

Ejemplo de aplicación
En éste ejemplo implementaremos las propiedades anteriores en una aplicación de la integral en crecimiento poblacional, para una mejor visualización.
Una población crece con una tasa de 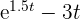 individuos por año (donde
individuos por año (donde  es el número de años). En el primer año la población es de 1500 personas.
es el número de años). En el primer año la población es de 1500 personas.
¿Cuánto creció la población entre en primer y tercer año?, ¿Cuál es la población en el tercer año?
1 Dado que nos pide el crecimiento de la población entre 1 y 3, es decir, el área bajo la curva de la tasa de crecimiento entre 1 y 3, lo expresaremos como sigue:

Nota: los pasos siguientes son para ilustrar el uso de las propiedades, algunos de ellos pueden ser omitidos.
2 Al hacer los cálculos, notemos que podemos usar la propiedad 4 y separamos en una suma.

3 También podemos utilizar la propiedad 5 y sacamos el la constante -3 que multiplica a t.
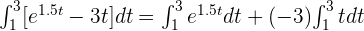
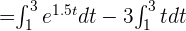
4 Dado que 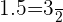 sustituimos y hacemos los cálculos que correspondientes para hallar la respuesta a la primera pregunta:
sustituimos y hacemos los cálculos que correspondientes para hallar la respuesta a la primera pregunta:

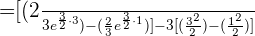
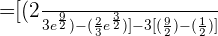
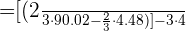

Así el crecimiento entre el primer y tercer año fue de 33 individuos aproximadamente.
6 Para la segunda pregunta seguimos es siguiente razonamiento:
- En el año 1 la población era de 1000 individuos.
- El crecimiento entre el año 1 y 3 fue de 33 individuos aproximadamente.
- Así la población al en el año 3 es de 1033 individuos aproximadamente.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio 26 el resultado no se ve bien, como quedaria?
Disculpa pero no hay ejercicio 26, solo llega al 20.
estan la mitad de los ejercicios incorrectos, revisarlos por favor
Podrías indicarnos que ejercicios están mal, pues ya revise y no encontre los errores.
En el ejercicio 13 que es la integral de x^2 * ln(x^2), al hacerlo por partes hace bien lo de coger como u=ln(x^2), pero al coger x^2 como v’ se equivoca y lo coge como x^3
Una disculpa ya se corrigió.
En la pagina no deja ver las respuestas, me parece que es un error de vosotros a ver si lo podeis arreglar, mil gracias
Hola, Pancracio:
Las soluciones ya aparecen correctamente 🙂
Un saludo
Estudio carrera de ingeniería pero me cuesta mucho las matemáticas ¿ algún consejo? O tips